Skip to main content

This notebook was created by Sergey Tomin (sergey.tomin@desy.de). April 2025.

Optics for High Time Resolution Measurements with TDS

This tutorial is motivated by a practical task: improving the time resolution of current profile measurements using a Transverse Deflecting Structure (TDS) at the European XFEL (EuXFEL).
The tutorial itself is available in Jupyter Notebook format and can be downloaded here.

The lattice files used in this tutorial can be found in this repository.

A Bit of Simple Theory​

The transverse position of a particle along a beamline is given by:

x(s)=Aβx(s)cos⁡(Φx(s)+Φ0)x(s) = A \sqrt{\beta_x(s)} \cos(\Phi_x(s) + \Phi_0)

where:

  • βx(s)\beta_x(s) is the betatron function at position ss,
  • Φx(s)=∫s0s1βx(s) ds\Phi_x(s) = \int_{s_0}^{s} \frac{1}{\beta_x(s)} \, ds is the betatron phase,
  • Φx′(s)=1βx(s)\Phi'_x(s) = \frac{1}{\beta_x(s)}.

Taking the derivative:

x′(s)=−Aβx(s)[αx(s)cos⁡(Φx(s)+Φ0)+sin⁡(Φx(s)+Φ0)],x'(s) = -\frac{A}{\sqrt{\beta_x(s)}} \left[ \alpha_x(s) \cos(\Phi_x(s) + \Phi_0) + \sin(\Phi_x(s) + \Phi_0) \right],

with αx(s)=−12βx′(s)\alpha_x(s) = -\frac{1}{2} \beta_x'(s).

At the TDS Position​

Let’s assume the TDS is located at s=0s = 0:

  • The particle receives a transverse kick: xtds′=x′(0)x'_{\text{tds}} = x'(0),
  • The transverse position at the TDS is zero: x(0)=0x(0) = 0.

Then:

0=Aβx(0)cos⁡(Φ0)⇒Φ0=π20 = A \sqrt{\beta_x(0)} \cos(\Phi_0) \Rightarrow \Phi_0 = \frac{\pi}{2}

From this, we get:

xtds′=−Aβx(0)⇒A=−xtds′βx(0)x'_{\text{tds}} = -\frac{A}{\sqrt{\beta_x(0)}} \Rightarrow A = -x'_{\text{tds}} \sqrt{\beta_x(0)}

At the Screen​

The transverse position on the screen becomes:

x(s)=Aβx(s)cos⁡(ΔΦx+Φ0)x(s) = A \sqrt{\beta_x(s)} \cos(\Delta\Phi_x + \Phi_0)

With Φ0=π2\Phi_0 = \frac{\pi}{2} and using the identity cos⁡(ψ+π/2)=−sin⁡(ψ)\cos(\psi + \pi/2) = -\sin(\psi):

xscr=xtds′βx(stds)βx(sscr)sin⁡(ΔΦx)x_{\text{scr}} = x'_{\text{tds}} \sqrt{\beta_x(s_{\text{tds}}) \beta_x(s_{\text{scr}})} \sin(\Delta\Phi_x)

Transverse Kick from the Deflecting Structure​

The kick from the TDS depends on time:

Δxtds′(t)=eV0pcsin⁡(2πctλ+φ)≈eV0pc(2πctλcos⁡φ+sin⁡φ)\Delta x'_{\text{tds}}(t) = \frac{e V_0}{p c} \sin\left( \frac{2\pi c t}{\lambda} + \varphi \right) \approx \frac{e V_0}{p c} \left( \frac{2\pi c t}{\lambda} \cos \varphi + \sin \varphi \right)

Assuming φ=0\varphi = 0 (zero-crossing), the rms beam size on the screen is:

σxscr=eV0pc⋅2πcσtλ⋅βx(stds)βx(sscr)⋅sin⁡(ΔΦx)\sigma_x^{\text{scr}} = \frac{e V_0}{p c} \cdot \frac{2\pi c \sigma_t}{\lambda} \cdot \sqrt{\beta_x(s_{\text{tds}}) \beta_x(s_{\text{scr}})} \cdot \sin(\Delta\Phi_x)

Time Resolution of the TDS​

Streaking (Calibration) Factor​

The streaking factor is:

S=σxscrcσt=eV0pc⋅2πλ⋅βx(stds)βx(sscr)⋅sin⁡(ΔΦx)S = \frac{\sigma_x^{\text{scr}}}{c \sigma_t} = \frac{e V_0}{p c} \cdot \frac{2\pi}{\lambda} \cdot \sqrt{\beta_x(s_{\text{tds}}) \beta_x(s_{\text{scr}})} \cdot \sin(\Delta\Phi_x)

Note that this expression can be written more compactly by recognizing that the corresponding element of the transfer matrix is:

R12=βx(stds)βx(sscr)⋅sin⁡(ΔΦx)R_{12} = \sqrt{\beta_x(s_{\text{tds}}) \beta_x(s_{\text{scr}})} \cdot \sin(\Delta\Phi_x)

or, if the streaking occurs in the vertical direction:

R34=βy(stds)βy(sscr)⋅sin⁡(ΔΦy).R_{34} = \sqrt{\beta_y(s_{\text{tds}}) \beta_y(s_{\text{scr}})} \cdot \sin(\Delta\Phi_y).

Thus, the streaking factor simplifies to:

S=σxscrcσt=eV0pc⋅2πλ⋅R12S = \frac{\sigma_x^{\text{scr}}}{c \sigma_t} = \frac{e V_0}{p c} \cdot \frac{2\pi}{\lambda} \cdot R_{12}

Time Resolution​

The time resolution is defined as:

Rt=σx0scrcSR_t = \frac{\sigma_{x0}^{\text{scr}}}{c S}

Using σx0scr=εxβx(sscr)\sigma_{x0}^{\text{scr}} = \sqrt{\varepsilon_x \beta_x(s_{\text{scr}})}, we get:

Rt=εxeV0p⋅2πλ⋅βx(stds)⋅sin⁡(ΔΦx)R_t = \frac{\sqrt{\varepsilon_x}}{\frac{e V_0}{p} \cdot \frac{2\pi}{\lambda} \cdot \sqrt{\beta_x(s_{\text{tds}})} \cdot \sin(\Delta\Phi_x)}

So the time resolution depends only on:

  • emittance εx\varepsilon_x
  • voltage V0V_0
  • wavelength λ\lambda
  • beta function at the TDS
  • phase advance between TDS and screen

Practical Example: Optimizing Time Resolution with TDS at EuXFEL​

In this section, we apply the theory from the previous part to a real EuXFEL lattice using Ocelot.

import sys 
sys.path.append("/Users/tomins/Nextcloud/DESY/repository/ocelot/")
import os
import copy
import pandas as pd

from ocelot import *
from ocelot.gui import *
import l2, l3 # lattices can be found in https://github.com/ocelot-collab/EuXFEL-Lattice/tree/main/lattices/longlist_2024_07_04

initializing ocelot...

Check design optics​

lat_l2 = MagneticLattice(l2.cell + l3.cell, stop=l3.bpmc_488_l3) # id_32072837_ - Drift in front of first A6 RF module
tws = twiss(lat_l2, tws0=l2.tws0)
plot_opt_func(lat_l2, tws, top_plot=["Dy"], legend=False)
plt.savefig("L2_design.png") 
plt.show()

png

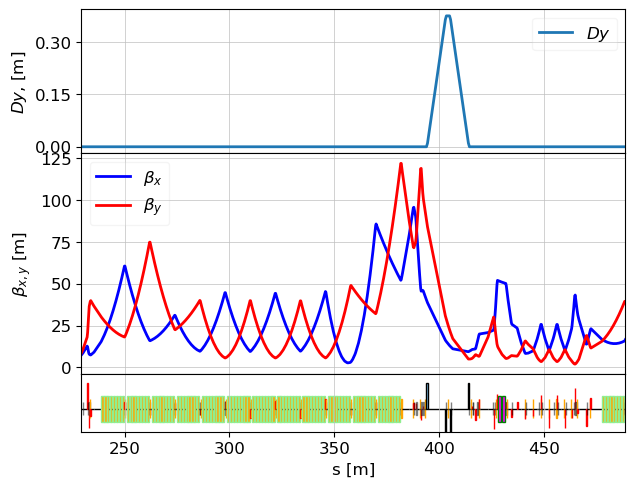
Check Twiss Parameters at Key Elements​

We use markers for the TDS and screens (e.g., marker_tds_b2, otrb_457_b2) and inspect relevant optics values like beta functions and phase advances.

tws = twiss(lat_l2, tws0=l2.tws0, attach2elem=True)
# with attach2elem=True to all elements will be attached Twiss object in element.tws
# let's print beta_x
print(l2.ensub_466_b2.tws.beta_y)

5.058664837892

Define Matching Start and End Points​

We preserve Twiss parameters at match_385_b2 (entry point after L2) and id_32072837_ (end of lattice).

END_ELEM = l3.id_32072837_

tws_match_385 = copy.deepcopy(l2.match_385_b2.tws)
tws_end = copy.deepcopy(END_ELEM.tws)

Shorten Lattice to Relevant Region​

We exclude upstream quadrupoles and start optimization just after L2.

lat = MagneticLattice(l2.cell+l3.cell, start=l2.match_385_b2, stop=END_ELEM)
tws_des = twiss(lat, tws0=tws_match_385)
plot_opt_func(lat, tws_des, top_plot = ["Dy"], legend=False)
plt.savefig("TDS_area_design.png")
plt.show()

png

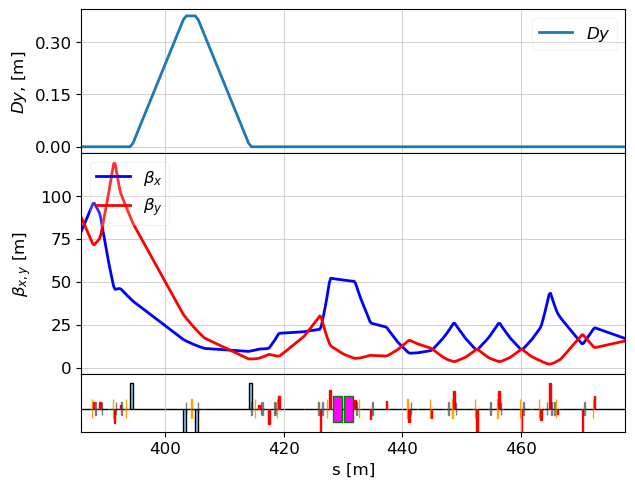
(Optional) Save Quadrupole Strengths for Reference​

We optionally store the design quadrupole strengths in a CSV file for comparison later. The function looks a bit complicated just because I wanted to avoid overwriting every time design quads strengths.

# let's save design kicks to a dictionary
df_filename = "quads_strengths.csv"
design_column = "design"
if os.path.exists(df_filename):
    quads_kicks_df = pd.read_csv(df_filename, index_col=0)
    if design_column in quads_kicks_df.columns:
        print(f"Column '{design_column}' already exists. Skipping step.")
    else:
        print(f"Column '{design_column}' not found. Proceeding to add it.")
        quads_kicks_df[design_column] = pd.Series(d_design)
        df.to_csv(df_filename)
else:
    print("File does not exist. Creating new DataFrame.")
    # let's save design kicks to a dictionary
    d_design = {}
    for e in lat.sequence:
        if e.__class__ == Quadrupole:
            d_design[e.id] = e.k1
    quads_kicks_df = pd.DataFrame({design_column: d_design})
    quads_kicks_df.to_csv(df_filename, index=True)

Column 'design' already exists. Skipping step.

Display Twiss Parameters at Specific Elements​

We define a helper function to show selected optics values and compute R12 matrix elements.

It can be done in different ways but we will use pandas.

# List of elements where we want to see Twiss parameters
elements_for_comparision = {'TDS 429': l2.marker_tds_b2, "Scr 450": l2.otrb_450_b2,  "Scr 454": l2.otrb_454_b2, 'Scr 457': l2.otrb_457_b2, 'Scr 461': l2.otrb_461_b2, 'end': END_ELEM}

# Attributes we want to compare
attributes = ['beta_x', 'beta_y', 'alpha_x', 'alpha_y', 'mux', "muy"]

def table_update(lat, tws0, elements_for_comparision, attributes):
    # calculate Twiss
    tws = twiss(lat, tws0=tws0, attach2elem=True)
    
    # Build the table from tws list
    table = pd.DataFrame({name: [getattr(getattr(obj, "tws"), attr) for attr in attributes] for name, obj in elements_for_comparision.items()},
                     index=attributes)
    # make phase advance in degree
    table.loc['mux'] = (table.loc['mux'] - table.loc['mux', 'TDS 429'])*180/np.pi
    table.loc['muy'] = (table.loc['muy'] - table.loc['muy', 'TDS 429'])*180/np.pi
    # add R12 elements into table 
    R12_values = copy.copy(elements_for_comparision)
    for key in R12_values:
        stop_elem = elements_for_comparision[key]
        _, R, _ = lat.transfer_maps(energy=2.4, start=l2.marker_tds_b2, stop=stop_elem)
        R12_values[key] = R[0, 1]
    table.loc['R12'] = R12_values
    return table
table = table_update(lat, tws_match_385, elements_for_comparision, attributes)
table
TDS 429Scr 450Scr 454Scr 457Scr 461end
beta_x50.9785817.0733616.9487417.0462317.1883916.88229
beta_y7.976265.969356.030835.977615.9844915.53650
alpha_x0.228632.13837-2.153392.13443-2.180460.43030
alpha_y0.89572-0.979541.00367-0.987360.98641-0.60920
mux0.0000071.6829488.3884998.69572115.29531157.32295
muy0.00000166.8764193.9847243.5603270.7594407.94331
R120.0000028.0073129.3826329.1398326.7630911.31032

Matching​

Objective: High Beta at TDS and 90° Phase Advance to Screen​

We now want to modify the optics such that:

  • The beta function at the TDS position is large (e.g., 120 m), which improves time resolution.
  • The phase advance between the TDS and screen is exactly 90 degrees.

To achieve this, we define a set of constraints and a list of quadrupoles we allow the matcher to modify.

constr = {
    l2.marker_tds_b2: {"beta_x": 150, "alpha_x": 0},
    l2.otrb_457_b2: {"beta_x": 17},
    "delta": {
        l2.marker_tds_b2: ["mux", 0],
        l2.otrb_457_b2: ["mux", 0],
        "val": np.pi / 2,
        "weight": 1_000_007
    },
}

vars = [
    l2.qd_417_b2, 
    l2.qd_418_b2, l2.qd_425_b2, l2.qd_427_b2,
    l2.qd_431_b2, l2.qd_434_b2, l2.qd_437_b2, l2.qd_440_b2,
    l2.qd_444_b2, l2.qd_448_b2, l2.qd_452_b2, l2.qd_456_b2
]

match(lat, constr, vars, tw=tws_match_385, verbose=False, max_iter=1000, method='simplex')
tws = twiss(lat, tws0=tws_match_385)
plot_opt_func(lat, tws, top_plot=["Dy"], legend=False)
plt.show()

initial value: x = [-0.7502347655006337, 0.6491929171989861, -1.3008034, 0.9414835846007605, 0.43518302749894383, -0.5278581910012674, 0.4055492834980989, -0.6685246719983101, -0.4582186614997888, 0.8960955489987327, -1.263284384000845, 0.8960955489987327] Optimization terminated successfully. Current function value: 0.000031 Iterations: 566 Function evaluations: 892

png

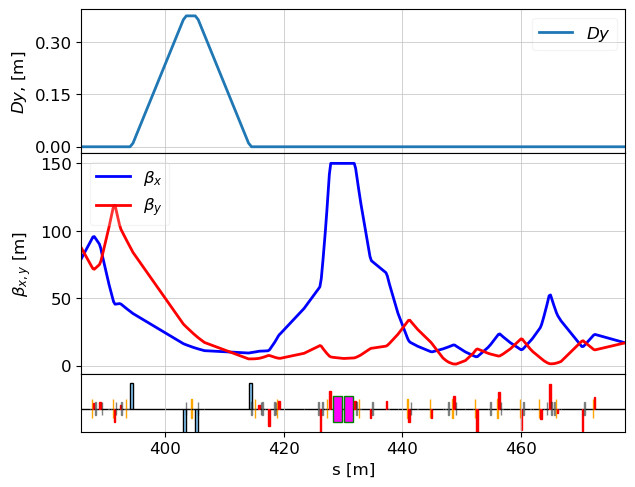
table = table_update(lat, tws_match_385, elements_for_comparision, attributes)
table
TDS 429Scr 450Scr 454Scr 457Scr 461end
beta_x149.9999910.1716913.4643217.0000020.5993316.91344
beta_y5.393193.806109.2571612.5352810.3520616.98702
alpha_x0.000011.20565-2.325241.64110-2.786590.43173
alpha_y0.07739-1.485900.75004-1.764352.13902-0.74985
mux0.0000053.1375578.5376290.00020104.86418144.32068
muy0.00000189.1443215.2306240.5480254.87936415.89824
R120.0000031.2517644.0441750.4975353.7267529.37750

Matching to Final Conditions​

We now restore the beam optics to match the original design values at the end of the beamline.

constr_end = {
    END_ELEM: {
        "beta_x": tws_end.beta_x,
        "beta_y": tws_end.beta_y,
        "alpha_x": tws_end.alpha_x,
        "alpha_y": tws_end.alpha_y
     },
    #     "delta": {
        
    #     l2.otrb_457_b2: ["mux", 0],
    #     END_ELEM: ["mux", 0],
    #     "val": (790-690.22)/180*np.pi,
    #     "weight": 1_000_007
    # },
}

vars_end = [
    l2.qd_459_b2, 
    l2.qd_463_b2, l2.qd_464_b2, l2.qd_465_b2,
    l3.qd_470_b2, l3.qd_472_b2
]

match(lat, constr_end, vars_end, tw=tws_match_385, verbose=False, max_iter=2000, method='simplex')
tws_hi_res = twiss(lat, tws0=tws_match_385)
plot_opt_func(lat, tws_hi_res, top_plot=["Dy"], legend=False)
plt.show()
table = table_update(lat, tws_match_385, elements_for_comparision, attributes)
table

initial value: x = [-1.263284384000845, -0.569607097600338, 1.2982678500000002, -0.24686100550063372, -1.1289067389987326, 0.6611797761005492] Optimization terminated successfully. Current function value: 0.000049 Iterations: 870 Function evaluations: 1359

png

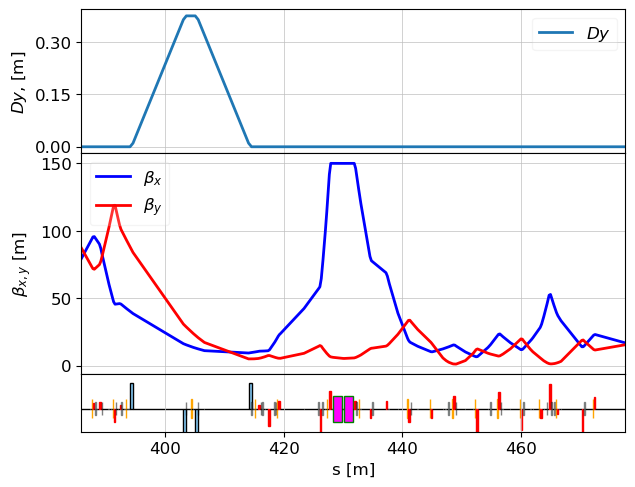
TDS 429Scr 450Scr 454Scr 457Scr 461end
beta_x149.9999910.1716913.4643217.0000020.7169916.88229
beta_y5.393193.806109.2571612.5352810.2463115.53648
alpha_x0.000011.20565-2.325241.64110-2.825210.43030
alpha_y0.07739-1.485900.75004-1.764352.15514-0.60920
mux0.0000053.1375578.5376290.00020104.84392144.39113
muy0.00000189.1443215.2306240.5480254.9183417.5666
R120.0000031.2517644.0441750.4975353.8850129.30015

Compare design and new optics​

bx_n = [tw.beta_x for tw in tws_hi_res]
by_n = [tw.beta_y for tw in tws_hi_res]
s_n = np.array([tw.s for tw in tws_hi_res])
bx_d = [tw.beta_x for tw in tws_des]
by_d = [tw.beta_y for tw in tws_des]
s_d = np.array([tw.s for tw in tws_des])

fig, ax = plot_API(lat, legend=False, figsize=[10,6])

ax.plot(s_n - s_n[0], bx_n, 'C0', label=r"hi res $\beta_{x}$ ")
ax.plot(s_n - s_n[0], by_n, 'C1', label=r"hi res $\beta_{y}$ ")
ax.plot(s_d - s_d[0], bx_d, "C0--", label=r"design $\beta_{x}$ ")
ax.plot(s_d - s_d[0], by_d, "C1--", label=r"design $\beta_{y}$ ")
ax.set_ylabel(r"$\beta_{x,y}$ [m]")
ax.legend()
#plt.savefig("TDS_90m.png") 
plt.show()

png

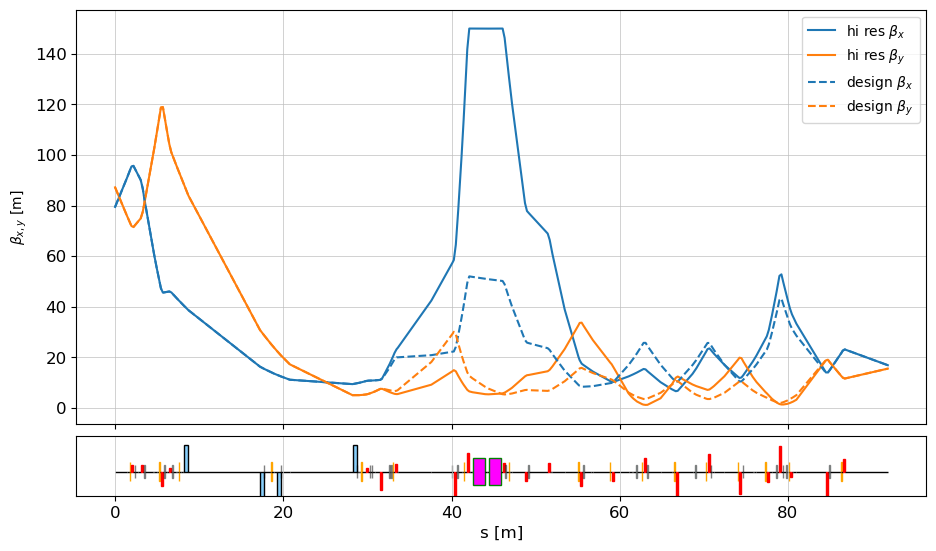
for key in ['beta_x', "beta_y", "alpha_x", "alpha_y"]:
    print(key, " :", getattr(tws_hi_res[-1], key), getattr(tws_des[-1], key))

beta_x : 16.882291323377554 16.882288192819743 beta_y : 15.536480497394853 15.536499055076685 alpha_x : 0.4302991727930746 0.4303020309015204 alpha_y : -0.6092012060842842 -0.609204409231985

Write to dataframe new quads kicks. Change name of new_colimn​

WRITE_TO_FILE = True
REWRITE = True

beta_tds_ampl = constr[l2.marker_tds_b2]["beta_x"] 
new_column = f'TDS {beta_tds_ampl}m'


quads_kicks_df = pd.read_csv(df_filename, index_col=0)
# let's save design kicks to a dictionary
d_new = {}
for e in lat.sequence:
    if e.__class__ == Quadrupole:
        d_new[e.id] = e.k1
if WRITE_TO_FILE:
    if new_column in quads_kicks_df.columns and not REWRITE:
        print(f"Column '{new_column}' already exists. Skipping step.")
    else:
        print(f"Column '{new_column}' not found. Proceeding to add it.")
        quads_kicks_df[new_column] = pd.Series(d_new)
        quads_kicks_df.to_csv(df_filename)

quads_kicks_df

Column 'TDS 140m' already exists. Skipping step.

QuaddesignTDS 70mTDS 90mTDS 120mTDS 140mTDS 150m
QD.387.B20.3351730.3351730.3351730.3351730.3351730.335173
QD.388.B20.3559960.3559960.3559960.3559960.3559960.355996
QD.391.B2-0.725525-0.725525-0.725525-0.725525-0.725525-0.725525
QD.392.B20.1969960.1969960.1969960.1969960.1969960.196996
QD.415.B20.1806860.1806860.1806860.1806860.1806860.180686
QD.417.B2-0.750235-0.784398-0.844188-0.925253-0.878182-0.971459
QD.418.B20.6491930.5847150.5296100.4622140.3370360.409773
QD.425.B2-1.300803-1.347249-1.304467-1.251303-1.156159-1.308911
QD.427.B20.9414840.9612470.9598890.9555790.9299760.990706
QD.431.B20.4351830.4383390.4485290.4466430.5008210.443519
QD.434.B2-0.527858-0.516594-0.534249-0.520934-0.612066-0.505477
QD.437.B20.4055490.4249190.4352920.4441770.4249770.443716
QD.440.B2-0.668525-0.694907-0.699210-0.737736-0.726803-0.745826
QD.444.B2-0.458219-0.453644-0.463892-0.485140-0.462831-0.499049
QD.448.B20.8960960.8300440.7882040.7583490.7144620.711105
QD.452.B2-1.263284-1.280195-1.307186-1.370400-1.379105-1.412015
QD.456.B20.8960960.9142910.9192210.9087250.9873460.937405
QD.459.B2-1.263284-1.365812-1.289895-1.160471-1.135981-1.168825
QD.463.B2-0.569607-0.516755-0.521682-0.541629-0.480187-0.536436
QD.464.B21.2982681.3081251.3169631.3356471.2305221.338992
QD.465.B2-0.246861-0.235193-0.244567-0.263073-0.241534-0.264049
QD.470.B2-1.128907-1.199967-1.210101-1.231144-1.292447-1.261294
QD.472.B20.6611800.6508040.6478350.6503710.7576290.660549

Check optics again from dataframe​

quads_kicks_df = pd.read_csv(df_filename, index_col=0)
quads = list(quads_kicks_df.index)
optics = list(quads_kicks_df.columns)

fig, (ax_extra, ax_xy) = plot_API(lat, figsize=(12,8), add_extra_subplot=True)
ax_extra.set_ylabel(r"$\beta_x$ [m]")
ax_xy.set_ylabel(r"$\beta_y$ [m]")
data = {}
for opt in optics:
    data[opt] = []
    for e in lat.sequence:
        if e.id in quads:
            e.k1 = quads_kicks_df[opt][e.id]

    tws = twiss(lat, tws0=tws_match_385)
    data[opt] = tws
    s = np.array([tw.s for tw in tws]) - tws[0].s
    bx = [tw.beta_x for tw in tws]
    by = [tw.beta_y for tw in tws]
    ax_extra.plot(s, bx, label=opt)
    ax_xy.plot(s, by, label=opt)
ax_xy.legend()
ax_extra.legend()
plt.show()

png

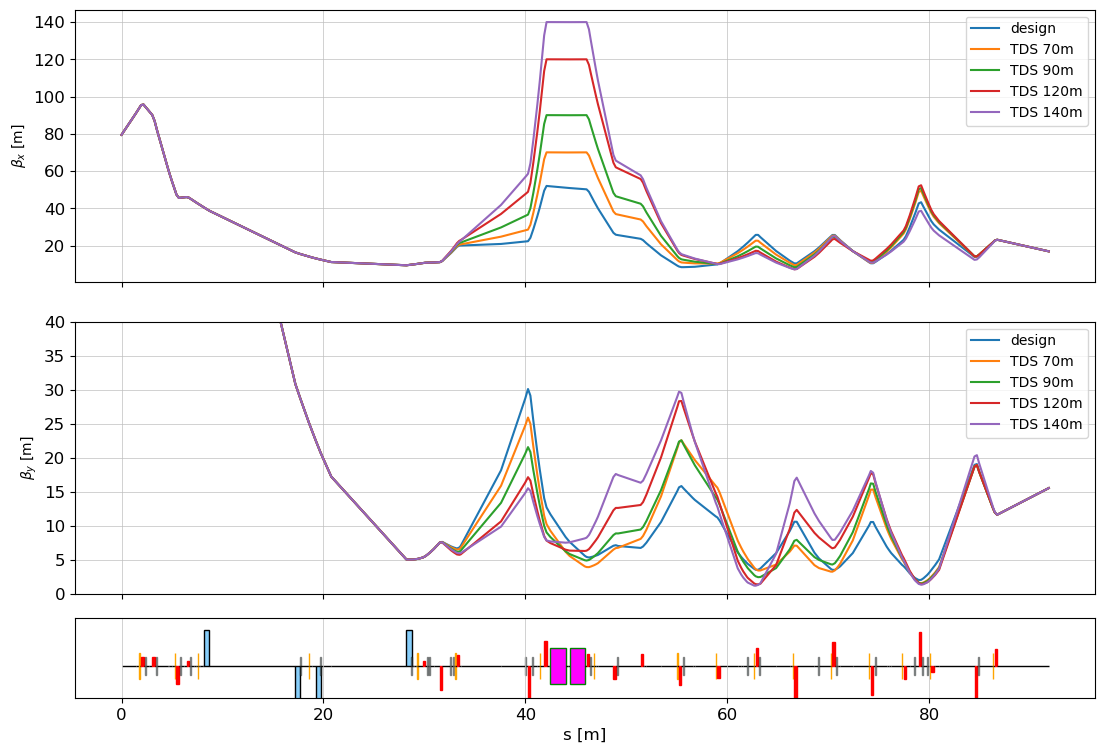
Let’s Put Some Numbers to Understand the TDS Voltage (Streaking/Calibration Factor)​

The streaking factor is given by:

S=σxscrcσt=eV0pc⋅2πλ⋅βx(stds)βx(sscr)⋅sin⁡(ΔΦx)S = \frac{\sigma_x^{\text{scr}}}{c \sigma_t} = \frac{e V_0}{p c} \cdot \frac{2\pi}{\lambda} \cdot \sqrt{\beta_x(s_{\text{tds}}) \beta_x(s_{\text{scr}})} \cdot \sin(\Delta\Phi_x)

or, as defined above, it can be rewritten using the transfer matrix element:

S=σxscrcσt=eV0pc⋅2πλ⋅R12S = \frac{\sigma_x^{\text{scr}}}{c \sigma_t} = \frac{e V_0}{p c} \cdot \frac{2\pi}{\lambda} \cdot R_{12}

During experimental study of the proposed optics, we measured a calibration factor of S=11.1S = 11.1 mm/ps for our S-band TDS (operating at 3 GHz). For optics TDS150m, we have R12=50.5R_{12} = 50.5 between the TDS and a screen (Scr 457). Let’s calculate the required TDS voltage:

f = 3e9 # [Hz] frequency of the S-band TDS
S = 11.1e-3/1e-12 # [mm/ps] → [m/s]
R12 = 50.5 
Lrf = speed_of_light /f
pc = 2400 # [MeV] 

V = S * Lrf * pc /(R12 * 2 * np.pi* speed_of_light)
print(f"TDS voltage = {V} MV")
    TDS voltage = 27.986057319921404 MV